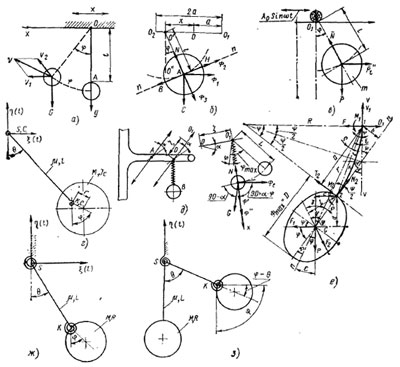
При колебании дерева плод на плодоножке может совершать колебания практически в любой плоскости. При этом на горизонтальное смещение точки подвеса плода могут накладываться смещения в вертикальной и других плоскостях. Сама ветвь также может вибрировать не в одной плоскости, поэтому абсолютное движение центра тяжести плода — это очень сложное движение, трудно поддающееся математическому описанию. Математический анализ движения центра тяжести плода возможен при наложении на систему плод – плодоножка некоторых ограничений, приводящих к ошибке в конечных результатах.
Отделение плодов от ветвей происходит в результате действия инерционных сил, возникающих от колебаний точки подвеса плода в горизонтальной или вертикальной плоскостях; соосной растягивающей силы; усталостных разрушений плодоножки в месте крепления к ветви или плоду, а также в результате кручения плода относительно места его прикрепления к плодоножке и других сложных деформаций плодоножки, которые до сих пор полностью не изучены. Основные возможные виды движения плодов при вибрационной уборке показаны на рис. 49. Во всех случаях отрыву плода соответствует определенное значение частоты возмущающей силы, обеспечивающей его необходимое угловое или вертикальное ускорение.
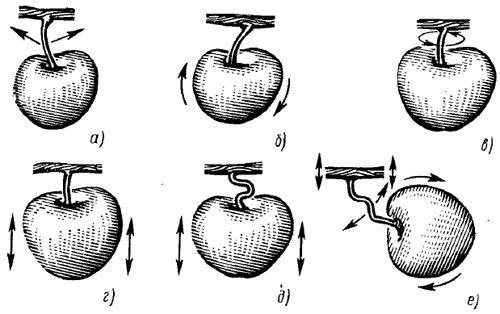
Рис. 49. Основные виды движения плода при вибрационной уборке:
а — маятниковое; б — качающееся; в — крутильное; г — вертикальное (рывковое); д — вертикальное (рывковое) с изгибом плодоножки; е — комбинированное
Д-р тех. наук X. А. Хачатрян и канд. техн. наук Р. Р. Ягубян, д-р техн. наук А. Ф. Ульянов и канд. техн. наук В. Д. Забросаев, канд. техн. наук С. И. Филимонов (рис. 50, а – в) рассматривали механизм отрыва отдельного плода, применяя уравнение движения простого физического маятника с горизонтальным синусоидальным перемещением его точки подвеса.
Рис. 50. Некоторые схемы математических моделей движения плода при вибрационной уборке фруктов:
а — по X. А Хачатряну и Р. Р. Ягубяну; б — по А. Ф. Ульянову и В. Д. Забросаеву; в — по С. И. Филимонову; г — по П. Пархомчуку и И. Куку; д — по Б. И. Турбину, Д. Бартеневу и Т. М. Соболевой; е — по Ж. Дипаола; ж — по И. Куку и Р. Ранду; з — по Р. Ранду и И. Куку.
Д-р техн. наук Б. И. Турбин, канд. техн. наук В. Д. Бартенев и Т. М. Соболева (рис. 50, д) в основу выявления механизма отрыва отдельного плода при механизированной уборке лоложили рабочую гипотезу о наличии упругой связи между плодом на плодоносящей веточке высшего порядка и ветвью более низкого порядка. Применяя затем уравнения Лагранжа II рода, авторы получили уравнение движения центра тяжести плода в функции угла поворота.
Из зарубежных исследователей вопросами теоретического обоснования отрыва плода занимались Ж. Дипаола, И. Кук, Р. Ранд, И. Пархомчук, Ж. Стефанелли, И. Стаффорд, Р. Динер, Е. Джакомелли. Ч. Юнг, Р. Фридли, В. Миллер, Ч. Морроу и др.
Проф. Ж. Дипаола и др. при рассмотрении отрыва плода систему сил, действующих на него, сводят к силам и моментам, приведенным к двум точкам (рис. 50, е): точке 1 — месту соединения плодоножки с ветвью и точке 2 — месту соединения плодоножки с плодом. Эту систему сил и моментов выражают затем шестью уравнениями с 16 неизвестными. Задаваясь далее гармоническим законом колебания точки подвеса плода, уравнением упругой линии плодоножки при ее изгибе и внося ряд допущений, уравнения приводят к выражениям с шестью неизвестными, которые используют для решения поставленной задачи.
И. Кук и Р. Ранд для определения оптимальной частоты отделения плодов при вибрационной уборке использовали линеаризованную модель (рис. 50, ж) плод — плодоножка с амплитудой угловых колебаний 3°, возбуждаемой одновременными периодическими горизонтальными и вертикальными колебаниями. Участки динамической неустойчивости и соответствующие формы моды выводились при помощи сдвоенных неоднородных уравнений Хиллса, описывающих движение двойного физического маятника с торсионными пружинами.
В результате анализа авторы установили, что оптимальным колебательным режимом движения системы плод – плодоножка (при наличии вертикального компонента возбуждения точки подвеса) будет такой, при котором вынужденная круговая частота равна удвоенной собственной частоте системы плод – плодоножка. В этом случае будет обеспечена высокая полнота съема плодов.
В другой работе Р. Ранд и И. Кук провели исследования системы плод – плодоножка с применением нелинейной теории динамики плодоножки и плода (рис. 50, з). Цифровое интегрирование сдвоенных нелинейных уравнений движения системы показало, что приблизительные аналитические результаты действительны для углов, равных 1 рад.
На основании проведенного анализа авторы пришли к выводу, что частота внутрифазовых собственных колебаний всех изученных плодов при вибрационной уборке не зависит от амплитуды собственных колебаний. При этом нелинейные влияния для этой моды неощутимы для углов отклонения до 30°. Для углов отклонения 90° собственная частота двойного маятника не совпадает с частотой эквивалентного простого нелинейного маятника, однако это несовпадение не превышает 15% в сторону уменьшения с учетом частоты наибольшего угла. С уменьшением же угла отклонения процент несовпадения частот также уменьшается.
И. Пархомчук и И. Кук рассмотрели характер отделения плодов с плодоножкой или без нее. При этом модель плода с плодоножкой уподоблялась двойному физическому маятнику (рис. 50, г). Установлено, что для малых отклонений движение двойного физического маятника может быть уподоблено движению физического маятника с одной степенью свободы.
И. Стаффорд и Р. Динер провели теоретические исследования по установлению границ частоты и амплитуды колебаний плодов, обеспечивающих необходимую полноту съема. Они нашли, что отрыв плодов яблок происходит при частоте 400 – 600 кол/мин, в 2 – 3 раза превышающей собственную частоту системы плод – плодоножка.
Ж. Стефанелли рассматривал теорию и упрощенную методику расчета параметров, действующих на систему плод – плодоножка. При этом рассмотрены самые простые случаи воздействия на плод и сделана попытка определить некоторые условия отрыва плода при помощи приближенных и пригодных только для ориентировочных оценок формул.
Отрыв плода от плодоножки (или плодоножки от ветви) может произойти в результате простых воздействий (растяжение, изгиб, кручение, срез), комбинированных (например, растяжение и изгиб; изгиб и кручение; изгиб и срез и др.) или усталостных явлений, вызываемых малыми, но многократно повторяющимися растягивающими, изгибающими, скручивающими и срезающими воздействиями.
Проводя анализ отрыва плода, автор рассматривал только простые воздействия в предположении, что связь плода с плодоножкой является совершенным соединением, хотя это во многих случаях вряд ли соответствует действительности.
Е. Джакомелли считает, что для уборки плодов вибрационными машинами главное значение имеет определение собственной частоты колебаний ветвей и прежде всего системы плод – плодоножка. Если собственная частота известна, то можно подобрать подходящую частоту колебания практически любого элемента системы (дерева, ветви и т. п.) для обеспечения высокой полноты съема плодов.
Ч. Юнг и Р. Фридли делают попытку разработать и оценить расчетную модель всего плодового дерева, что, по их мнению, позволит более точно представить колебательную характеристику всей системы (дерево – ветвь – плодоножка – плод). Для раскрытия качественной стороны вопроса авторы использовали метод ограниченного элемента. В результате сравнительно сложного анализа авторы пришли к выводу, что метод ограниченного элемента по определению собственных частот плодового дерева обеспечивает достаточно высокую сходимость результатов с экспериментальными данными.
В. М. Миллер и Ч. Т. Морроу делают попытку математическим путем получить вибрационную характеристику системы плодоножка — яблоко, чтобы определить возможность отрыва плода с плодоножкой или без нее. Для исследований они применяли моделирование системы с одной степенью свободы. При этом плодоножку принимали абсолютно жесткой и считали, что точка подвеса получает синусоидальное осевое (вертикальное) возбуждение. Эксперименты были проведены лишь в лабораторных условиях. В полевых условиях такие эксперименты осуществить трудно, так как в настоящее время пока еще нет возбудителей колебаний, которые бы вызывали на плодовом дереве только вертикальные колебания плодов.
Почти все зарубежные исследователи (за исключением Ж. Стефанелли) для оценки отрыва плода проводят сравнительно сложный анализ, получают громоздкие окончательные расчетные формулы, а затем указывают, что результаты, найденные по упрощенным формулам, отличаются на 10 – 15%. Исходя из этого, для оценки условий отрыва плода можно применять простые расчетные формулы, вместо двойного физического маятника рассматривать простой и формулы, полученные для углов отклонения плода до 3° от вертикали, с небольшой погрешностью применять для углов отклонения до 1 рад и т. д.
В работах автора данной книги ставилась задача найти упрощенную теорию отрыва плода, которая хорошо подтверждалась бы экспериментальными исследованиями и могла быть использована конструкторскими организациями для выбора режимов работы вибраторов плодоуборочных машин, обеспечивающих высокую полноту съема плодов. В связи с этим главными вопросами при решении данной задачи были установление закона движения точки подвеса плода и выбор основного вида колебания плода на плодоножке.
Как уже было указано, предполагалось, что точка подвеса плода, независимо от расположения на ветви, при колебании последней совершает горизонтальные гармонические колебания. Это предположение подтверждено опытным путем.
Кратко рассмотрим правомерность некоторых других принятых допущений. При анализе колебательной системы плод – плодоножка пренебрегали массой плодоножки. Для крупных (яблоки, груши и т. п.) и средней крупности (сливы, абрикосы, грецкие орехи, персики и т. п.) плодов это допущение вполне правомерно, так как масса плодоножки крупных плодов в 40 – 120 раз меньше массы плода, а масса плодоножки плодов средней крупности в 17 – 34 раза. Несколько проблематичнее такое допущение для вишни и черешни, так как масса их плодоножек только в 3 – 5 раз меньше массы плодов. Таким образом, для крупных и средней крупности плодов центр тяжести системы плод – плодоножка с погрешностью до 0,5% может быть принят в центре тяжести плода, представленного в виде шара, т. е. в центре шара. Подобное допущение принято и для плодов вишни и черешни, хотя у них из-за соизмеримости масс плодоножки и плода центр тяжести системы плод – плодоножка может быть несколько смещен в сторону места стыка плода с плодоножкой. Возможность такого допущения должна быть проверена экспериментально.
При пренебрежении массой плодоножки (делая ее невесомой) физический маятник (система плод – плодоножка) как бы переводится в математический. Однако для математического анализа он может быть принят с небольшой погрешностью (до 3%) в качестве физического маятника.
Предположение о шарнирном соединении плодоножки с ветвью (т. е. о совершенном соединении) дает определенную ошибку в окончательных результатах, которая не превышает 3%.
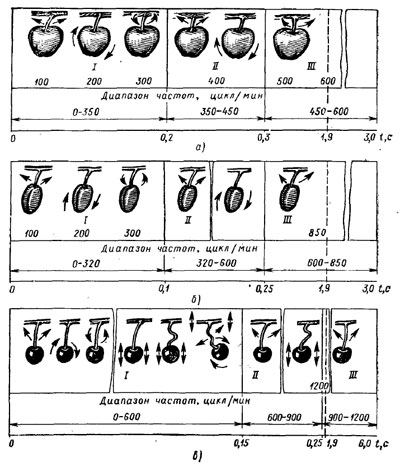
В качестве основного вида колебаний плодов при механизированной уборке принимаем маятниковый (см. рис. 49). При этом исходим из следующих соображений: при колебании дерева плод на плодоножке и сама ветвь могут совершать колебания в любой плоскости, поэтому абсолютное движение центра тяжести плода будет очень сложным. Особенно сложные движения плода с изгибом плодоножки наблюдаются при уборке вибрационным способом мелких плодов с длинными плодоножками (вишни, черешни, оливы и др.). Крупные плоды (яблоки, груши и др.) и плоды средней крупности (сливы, абрикосы, мелкие яблоки и др.), имеющие сравнительно недлинные плодоножки, прочно связанные с плодом, совершают более устойчивые колебания в основном маятникового типа (рис. 51).
Учитывая, что под семечковыми культурами с крупными плодами занято около 72% общих площадей садов в стране, под косточковыми культурами с плодами средней крупности около 18% площадей, под косточковыми культурами с мелкими плодами около 4% площадей, можно без больших погрешностей в качестве основного вида колебаний плодов при вибрационной уборке принять маятниковый.
Таким образом, при математическом анализе механизма отрыва плода применено уравнение движения простого физического маятника с горизонтальным синусоидальным перемещением точки подвеса. Зная закон движения центра тяжести плода, а также некоторые физико-механические свойства плодов (прочность связи плодоножки с ветвью и плодом, размеры и массу плода и плодоножки), можно прогнозировать наивыгоднейшие режимы колебаний точки подвеса плода для его отрыва путем теоретического подсчета инерционных сил при различных режимах колебаний и последующего сравнения их со статическими усилиями отрыва плодов. Если инерционные силы будут больше статических усилий отрыва, то плод оторвется в месте наименьшей связи.
Вынужденные колебания маятника с горизонтальным перемещением точки подвеса можно уподобить движению маятника, точка подвеса которого прикреплена к поступательно движущейся платформе (рис. 52). Вначале рассмотрим общую теорию маятника на платформе, поступательно движущейся по любому закону. Соединим с платформой систему координат О'Х'У' и зададим поступательное движение платформы уравнением движения начала О' по отношению к неподвижной системе OXY. Дифференциальные уравнения движения маятника получаем как методом Лагранжа, так и непосредственно составлением дифференциальных уравнений относительного движения (с учетом инерционных сил).
Рис. 51. Режимы движения плодов при вибрационной уборке:
а — яблоки; б — сливы, абрикосы, грецкие орехи; в — вишня, черешня; I — сильно неустойчивый, полнота съема яблок до 5%, слив, абрикосов, грецких орехов до 3%, вишни, черешни до 20%; II — неустойчивый, полнота съема яблок до 10%, слив, абрикосов, грецких орехов до 7%, вишни, черешни до 25%; III — устойчивый, общая полнота съема яблок до 97%, слив, абрикосов, грецких орехов до 98%, вишни, черешни до 95%. Полнота съема плодов при режимах I – III дана нарастающим итогом
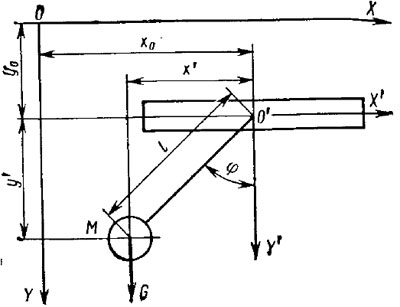
Рис. 52. Маятник на поступательно движущейся платформе
Остановимся вначале на методе составления уравнений Лагранжа. За обобщенную координату примем угол φ отклонения маятника от оси О'У".
Тогда координаты абсолютного движения точки М будут
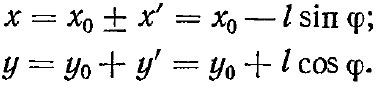
Определяем кинетическую энергию, пользуясь только что, полученными равенствами. Для этого сначала находим
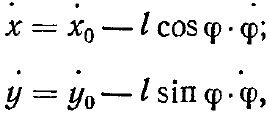
а затем уже получаем
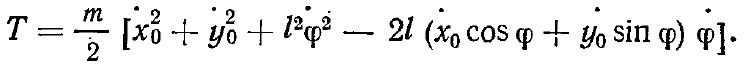
Потенциальная энергия будет
![]()
Составляем далее уравнение Лагранжа
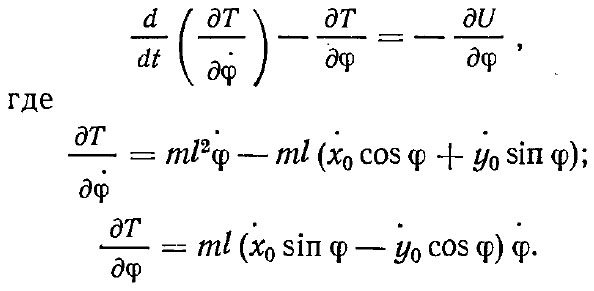
Подставляя значения величин в уравнение Лагранжа, получаем
![]()
Это же уравнение вытекает и из рассмотрения поступательного движения точки М. В этом случае к грузу G необходимо сначала прибавить силу инерции переносного движения, в данном случае поступательного движения относительно системы, равную — mj0. Проекции этой силы инерции на неподвижную ось координат будут ![]()
Применяя теорему моментов количества движения относительно точки О', получаем
![]()
Выразив х' и у' через l и φ, имеем вновь дифференциальное уравнение (1).
При колебании платформы в горизонтальной плоскости по гармоническому закону xo = a sin vt, yо = 0 дифференциальное уравнение движения (1) имеет следующий вид:
![]()
В случае малых колебаний можно принять sinφ≈φ; cos φ≈1. Обозначив g/l = w2, окончательно получим выражение, являющееся уравнением вынужденных колебаний:
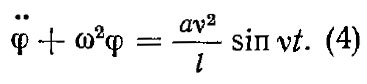
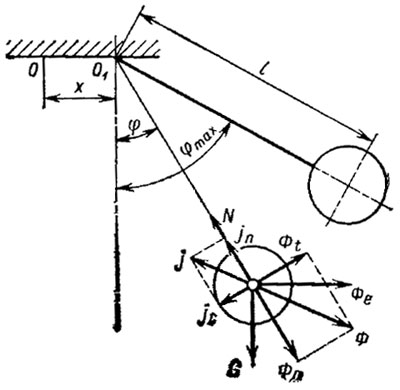
Рис. 53. Схема сил, приложенных к плоду при его колебаниях
Решение уравнение (4) в силу его линейности может быть представлено в виде суммы φ = φ1 + φ2, где φ1 — общий интеграл соответствующего однородного уравнения ![]() φ2 — частное решение данного неоднородного уравнения.
φ2 — частное решение данного неоднородного уравнения.
Общий интеграл однородного уравнения ![]() является уравнением собственных колебаний системы, интеграл которого будет φ1 = С1 sin ωt + C2 cos ωt, а частное решение может быть найдено в виде φ2 = B sin vt, где В — произвольная постоянная.
является уравнением собственных колебаний системы, интеграл которого будет φ1 = С1 sin ωt + C2 cos ωt, а частное решение может быть найдено в виде φ2 = B sin vt, где В — произвольная постоянная.
На основании этого можно записать
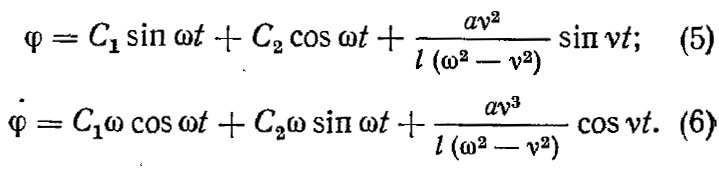
Постоянные интегрирования C1 и С2 определяют из начальных условий. При t = 0 φ = 0, откуда С2 = 0; при t = 0 φ = 0, откуда
![]()
Подставляя значения постоянных интегрирования в уравнение (5), окончательно получаем
![]()
где a — амплитуда возбуждающей силы; v — круговая частота возбуждающей силы; φ — угол отклонения маятника; l — приведенная длина физического маятника; ω = √g/l — круговая частота собственных колебаний.
Уравнение (7) является законом движения маятника (плода) в функции угла поворота. Как видно из этого уравнения, движение плода является результатом сложения двух гармонических колебаний, собственных и вынужденных, имеющих в общем случае различные амплитуды, частоты и фазы.
Из рис. 53 видно, что на отрыв плода во время колебания оказывают влияние нормальная Фn и касательная Фt составляющие силы инерции (8):
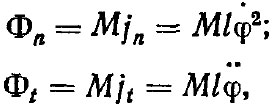
где М — масса плода; jn — нормальное ускорение; jt — касательное ускорение; φ• — угловая скорость; φ•• — угловое ускорение.
Полная сила инерции![]()
Для подсчета составляющих сил инерции Фn и Фt необходимо найти угловую скорость φ• и угловое ускорение φ•• плода.
Для получения φ• и φ•• дифференцируем уравнение (7) по времени
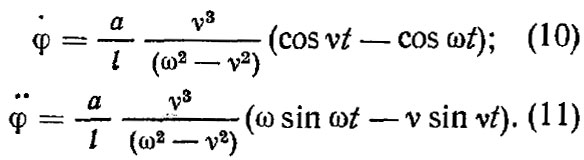
Составляющие силы инерции с учетом выражений (10) и (11) имеют вид
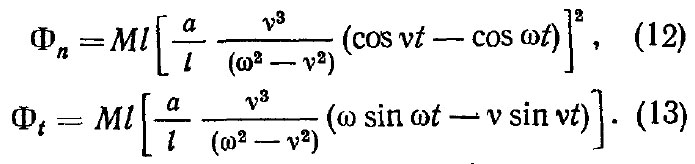
С использованием выведенных здесь формул на ЭВМ «Наири» проведены расчеты по прогнозированию оптимальных частотно-амплитудных режимов колебаний точки подвеса для отрыва плодов трех разновидностей: мелких косточковых (черешня, вишня), средних косточковых и орехоплодных (слива, миндаль, орех) и семечковых (яблоки, груши). При этом средняя масса плода принята у черешни и вишни равной 4 г; у слив, миндаля и орехов 30 г; у яблок и груш 80 г, а средняя приведенная длина физического маятника — соответственно 4,8; 3 и 4 см.
В результате расчетов получены частота колебаний для вишни и черешни 850 – 1100 циклов в минуту при амплитуде колебаний 20 – 30 мм; для слив, миндаля и орехов — 600 – 800 циклов в минуту при амплитуде 40 – 50 мм; для яблок и груш — 500 – 550 циклов в минуту при амплитуде 20 – 40 мм.
Изучение физико-математических показателей плодов и плодоножек, экспериментальное определение собственной частоты колебаний различных плодов, которая значительно (в 6 – 10 раз) ниже частоты вынужденных колебаний плода для его отрыва, подсчеты реакции натяжения плодоножек у различных плодов при их собственных колебаниях (у яблок максимальное усилие в плодоножке при собственных колебаниях равно 0,20 кгс, при отрыве плодоножки от ветви 2,35 кгс, у слив соответственно 0,08 и 1,3 кгс, у вишни и черешни 0,01 и 1,4 кгс) позволили высказать гипотезу о том, что наибольшее значение силы инерции в результате действия собственных колебаний; плода при его уборке вибрационным способом составит не более 10% от наибольшего значения силы инерции в результате его вынужденных колебаний.
Подобное предположение позволяет (с учетом условий 0≤|ω sin ωt| ≤2 и 0≤|v sin vt|≤20) в выражениях (10) и (11); пренебречь членом, содержащим частоту собственных колебаний, а величину (ω2 — v2) приравнять v2. Тогда эти выражения могут быть записаны в виде
![]()
а это в свою очередь позволяет выразить составляющие силы инерции Фn и Фt следующим образом:
![]()
С использованием последних выражений на ЭВМ «Наири» проведены необходимые расчеты по определению амплитудное частотных режимов колебаний точки подвеса для отрыва плода. Расчеты выполнены для тех же плодов и с теми же размерно-массовыми показателями, что и при расчете режимов колебаний точки подвеса с учетом наличия собственных колебаний плода.
В результате расчетов получены: для вишни и черешни частота колебаний 900 – 1200 циклов в минуту при амплитуде 20 – 30 мм, для слив, миндаля и орехов — 620 – 850 циклов в минуту при амплитуде 40 – 50 мм, для яблок и груш — 500 – 600 циклов в минуту при амплитуде 20 – 40 мм.
Сравнивая результаты расчетов необходимых режимов колебаний точки подвеса плода для его отрыва, видим, что расхождения по частоте колебаний составляют 10 – 15%, а расхождения по амплитуде колебаний отсутствуют. Таким образом, гипотеза полностью подтвердилась. Собственные колебания плода увеличивают динамические силы его отрыва на 10 – 15%.
Наличие большого числа случайных факторов при уборке плодов (расположение плодов на ветвях, характер их прикрепления, разница в размерно-массовых характеристиках плодов на одном дереве, кривизна ветвей и т. д.) дает основание полагать, что при прогнозировании необходимых режимов колебаний точки подвеса плода для его безусловного отрыва могут быть рекомендованы в первом приближении при расчетах составляющих сил инерции,выражения (15).
На основании анализа имеющихся материалов по отрыву плода, а также собственных исследований можно сказать, что в настоящее время в первом приближении создана теория отрыва плода при вибрационной уборке. Однако необходимы дополнительные теоретические исследования, чтобы предложить теорию, полностью отвечающую требованиям при создании плодоуборочных машин различного принципа действия.
Экспериментальные исследования показывают достаточно высокую сходимость результатов по частотно-амплитудным режимам для безусловного отрыва плода, подсчитанным по простым формулам и полученным опытным, путем.
Усложнение математических моделей путем представления системы плод – плодоножка в виде двойного физического маятника с торсионными пружинами в месте стыка плодоножки с плодом и ветвью приводит к получению более точных результатов по необходимой частоте и амплитуде колебаний точки подвеса плода для его отрыва. Однако сами же исследователи таких систем приходят к выводу, что можно в качестве модели принимать простой физический маятник, так как несовпадение требуемых для отрыва плода частот не превышает 15%.
Упрощенные формулы для расчета условий отрыва плода, полученные для углов отклонения плода до 3° от вертикали, могут быть с небольшой погрешностью применены, по данным американских ученых, для углов отклонения до 1 рад, по исследованиям автора — до 45°.