Как уже было указано ранее, для колебания деревьев (ветвей) в вибрационных полодоуборочных машинах применяют устройства различного типа. Основными узлами этих устройств являются вибраторы и захватные устройства (в дальнейшем будем называть их просто захватами).
Для эффективного съема плодов необходимо знать взаимодействие вибраторов с деревом, т. е. знать, какая часть заданной амплитуды колебаний вибратора передается дереву, что позволит правильно спроектировать необходимый для данных условий работы вибратор.
Вибраторы, применяемые для механизированной уборки плодов, могут быть разделены на четыре основных типа:
- вибраторы постоянного смещения — с кривошипно-шатунным механизмом и механическим или гидравлическим приводом;
- инерционные вибраторы — с механическим или гидравлическим приводом; в качестве исполнительного органа в таких вибраторах может быть использован кривошипно-шатунный механизм, одна неуравновешенная масса, две зависимые или две независимые неуравновешенные массы;
- кулачковые вибраторы — с механическим или гидравлическим приводом;
- импульсные вибраторы — с пневматическим или гидравлическим приводом.
Наибольший интерес для конструкторов плодоуборочных машин представляют вибраторы первого, второго и третьего типов, нашедшие преимущественное распространение в машинах.
Рассматривая взаимодействие вибраторов постоянного смещения, в качестве исполнительного рабочего органа в которых применен кривошипно-шатунный механизм, полагаем, что промежуточное звено (от места соединения с шатуном до захвата) — вибрирующий шток, осуществляющее передачу колебаний захвату, а значит, и дереву (ветви), абсолютно жесткое и не влияет на характер движения всей колебательной системы.
В общем случае сила, которая может быть сообщена дереву (ветви) вибратором постоянного смещения с исполнительным органом в виде кривошипно-шатунного механизма, определяется вторым законом Ньютона.
В машинах штангового типа вибраторы постоянного смещения с кривошипно-шатунным механизмом жестко крепят на тракторе. При вибрационной уборке плодов получается система, состоящая из трактора с машиной и дерева. При этом в машину входит рама с навешенным на нее вибратором, стрела с вибрирующим штоком внутри и захватное устройство.
При взаимодействии этой системы заданная амплитуда, колебаний частично передается дереву, частично гасится за счет горизонтального перемещения трактора.
Для построения математической модели принята система, состоящая из следующих элементов (рис. 42): трактор массой m1, стоящий на колесах с шинами, обладающими в горизонтальном направлении коэффициентом жесткости С1; дерево с приведенной к месту обхвата массой m2, обладающее коэффициентом жесткости С2, при отклонении его в горизонтальном направлении захватом машины; на тракторе укреплен вибратор, колеблющий горизонтально расположенную штангу по закону r cos vt. На конце штанги закреплен захват, охватывающий ствол дерева через упругую прокладку, обладающую коэффициентом жесткости С.
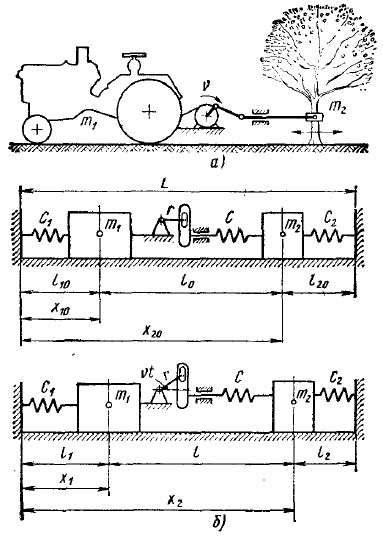
Рис. 42. Схема взаимодействия стрелы плодоуборочной машины, навешенной на трактор, с деревом: а — схема присоединения стрелы к дереву; б — эквивалентная схема колебательной системы
На этой же схеме x1 — координата трактора; х2 — координата дерева; q1 = х1 — x10 — отклонение массы трактора от нейтрального положения; q2 = x2 — x20 — отклонение массы дерева от нейтрального положения.
Дифференциальные уравнения движения масс находим с использованием уравнений Лагранжа II рода. Для этого сначала определяем кинетическую и потенциальную энергию системы.
Кинетическая энергия системы с учетом принятых обозначений
![]()
При отклонении трактора и дерева вправо на расстояния q1 и q2 и при повороте кривошипа вибратора от горизонтального положения против часовой стрелки на угол vt может быть отмечено следующее мгновенное изменение положения системы:
первая пружина (назовем ее тракторной) с коэффициентом жесткости C1 окажется растянутой на величину λ1 = q1, ее потенциальная энергия
U1 = C1q12/2;
вторая пружина (назовем ее пружиной дерева) с коэффициентом жесткости С2 окажется сжатой на величину λ2 = —q2, ее потенциальная энергия
U2 = C2q22/2;
третья пружина (назовем ее пружиной эластичного покрытия захвата) с коэффициентом жесткости С окажется растянутой на величину λ = q2 — q1 — r(1 — cos vt); ее потенциальная энергия
U3 = Сλ2/2 = С [q2 — q1 — r (1 — cos vt)] 2/2.
Потенциальная энергия всей системы
![]()
Уравнения Лагранжа II рода для рассматриваемой системы имеют вид
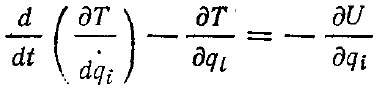
Эта колебательная система имеет три степени свободы. Однако одна из них — угол vt поворота кривошипа вибратора — заданная функция времени (кинематическое возбуждение).
В связи с этим достаточно составить два уравнения Лагранжа для координат q1 и q2, из которых могут быть найдены необходимые величины.
Записав составляющие уравнений Лагранжа и проведя преобразования, получим дифференциальные уравнения движения обеих масс
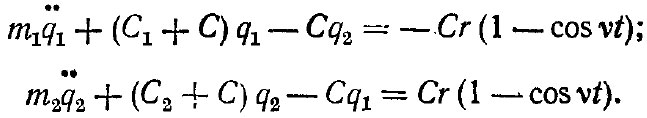
Вводя необходимые обозначения и считая, что начальные условия нулевые, т. е. ![]() , подвергая систему уравнений преобразованию Лапласа, получаем квадраты амплитудно-частотных характеристик масс дерева и трактора, из которых определяем отношение амплитуд колебаний дерева А2 и трактора А1:
, подвергая систему уравнений преобразованию Лапласа, получаем квадраты амплитудно-частотных характеристик масс дерева и трактора, из которых определяем отношение амплитуд колебаний дерева А2 и трактора А1:
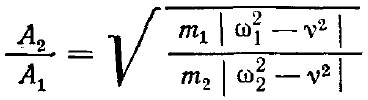
где ω12 =C1/m1 и ω22 =C2/m2 — квадраты собственных частот колебаний трактора и дерева.
Зная отношение амплитуд, можно получить сами амплитуды перемещения масс из условия А1 + А2 = r (где r — радиус кривошипа).
Решая совместно эти уравнения, получим
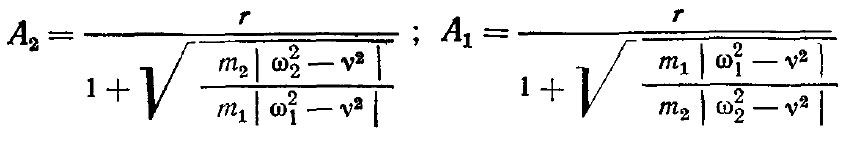
Условие А1 + А2 = r справедливо при предположении, что упругая прокладка захвата обеспечивает взаимное смещение захвата и ствола дерева намного меньшее, чем радиус кривошипа. Это предположение подтверждено проведенными экспериментами.
Представляя дерево в виде консоли переменного сечения и определяя приведенную массу mпр на любом расстоянии l от места заделки, необходимо помнить, что обязательным условием приведения является равенство собственных частот балок с равномерно распределенной нагрузкой и с сосредоточенной. Приведенную массу определяют по известной формуле С. П. Тимошенко
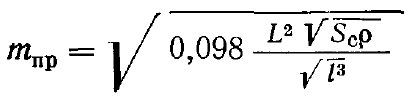
В этой формуле величинами L и l задаются, плотность ρ древесины определяют экспериментальным путем. Для всех плодовых деревьев без больших погрешностей может быть принята ρ = 0,001 кг/см3. Площадь поперечного сечения стержня Sc определяют исходя из конкретных условий приведения. В случае конического стержня его сначала приводят к цилиндрическому, находят радиус (диаметр) стержня и затем вычисляют площадь поперечного сечения образца.
С учетом изложенного амплитуды перемещений масс дерева и трактора, выраженные через коэффициенты жесткости дерева и трактора, могут быть написаны так:
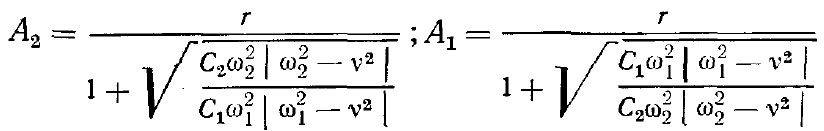
Коэффициент жесткости С2 дерева в месте обхвата определяют экспериментально (рис. 43).
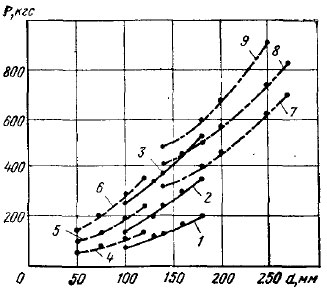
Рис. 43. Усилия, необходимые длч передачи вибрации стволам (штамбам) плодовых деревьев различного, диаметра:
1 – 3 — яблони и сливы в возрасте 11 лет при обхвате стволов (штамбов) на высоте соответственно 1,2; 0,8; 0,5 м от земли; 4 – 6 — полукустовидная вишня в возрасте 17 лет при обхвате стволов на высоте соответственно 0,6; 0,4; 0,3 м от земли; 7 – 9 — яблони и сливы в возрасте 25 лет при обхвате стволов на высоте соответственно 0,7; 0,6; 0,4 м от земли. Значения усилия даны при отклонении ствола в месте обхвата на 20 мм
Расчеты по указанным формулам показали, что 22 – 25% заданной амплитуды вибратора, установленного на тракторе класса 0,9 тс, не передается на дерево в месте его обхвата. Эксперименты полностью подтвердили теоретические выкладки.
В последнее время широко применяют на плодоуборочных машинах инерционные вибраторы с исполнительным органом в виде кривошипно-шатунного механизма. Такие устройства для колебания (ветвей) обычно называют стряхивателями турельного типа. Стрела устройства, внутри которой перемещается вибрирующий шток, шарнирно закреплена на специальном кронштейне, имеющем возможность поворачиваться на 360°, что улучшает маневренность устройства при обхвате ствола (ветви).
Взаимодействие стряхивателей турельного типа с деревьями несколько отличается от только что изложенного. С учетом работы рассмотрим основы теории движения, вызываемого в стволе (ветви) инерционным вибратором кривошипно-шатунного типа. При этом примем следующие допущения: система имеет одну степень свободы; сила упругости системы пропорциональна силе отделения плода; сила затухания пропорциональна скорости; возникшие колебания находятся в стабильной фазе, а вибратор способен аккумулировать энергию.
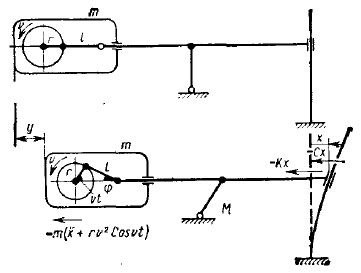
Рис. 44. Силы действующие в системе дерево-вибратор, при колебании дерева инерционным вибратором кривошипно-шатунного типа
В соответствии с рис. 44 запишем уравнение движения корпуса вибратора массой т для смещения ствола дерева на величину х
![]()
В этом уравнении и на рис. 44 приняты следующие обозначения: х, у — мгновенный сдвиг с позиции равновесия соответственно дерева и корпуса вибратора; т — масса корпуса вибратора; М — общая масса системы (масса вибратора и дерева); С — коэффициент упругости дерева; К — коэффициент затухания колебания дерева.
Взяв вторую производную от этого уравнения и считая, что l ≥ r, запишем ускорение корпуса вибратора в следующем приближенном виде:
![]()
Уравнение движения ствола (ветви) в месте захвата
![]()
Решение этого дифференциального уравнения второго порядка может быть получено в виде
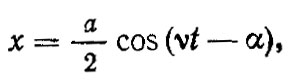
где a — амплитуда колебаний; α — фазовый угол.
Амплитуда колебаний может быть определена по формуле Томпсона
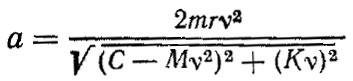
Экспериментально установлено, что частота вынужденных колебаний v значительно выше собственной частоты ω уравнение запишем в виде
а = 2mr/М.
Для подбора необходимой массы корпуса инерционного вибратора надо знать условия его работы, т. е. усредненные размерно-массовые показатели деревьев. Затем, задаваясь амплитудой колебаний вибратора (из предположения передачи, например, не менее 80% этой амплитуды дереву или ветви) можно легко определить требуемую массу корпуса вибратора.
Для колебания плодовых деревьев за штамб наибольшее применение находят-инерционные эксцентриковые вибраторы с двумя неуравновешенными (сосредоточенными) массами, вращающимися в противоположных направлениях.
Конструктивное оформление этих вибраторов крайне разнообразно, и каждый тип вибратора практически рассчитывают самостоятельно с учетом конкретных условий работы.
В общем случае инерционная сила F, возбуждаемая инерционным вибратором с двумя сосредоточенными массами (рис. 45), изменяется по гармоническому закону
F = 2mrv2 sin Θ.
Рассмотрим динамику инерционного вибратора с двумя неуравновешенными грузами, вращающимися в противоположных направлениях, при взаимодействии его с деревом.
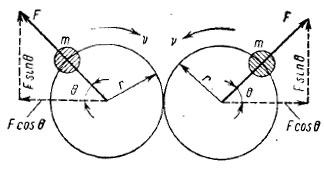
Рис. 45. Схема инерционного вибратора с двумя сосредоточенными массами
Рассмотрим динамику инерционного вибратора с двумя неуравновешенными грузами, вращающимися в противоположных направлениях, при взаимодействии его с деревом.
Схема динамической модели инерционного вибратора нагружающего дерево при возбуждении колебаний, показана на рис. 46. На схеме приняты следующие обозначения: m1 — обобщенная масса дерева и вибратора; m/2 —масса сосредоточенного груза; х — координата динамических перемещений нагруженного дерева вместе с вибратором; φ — угловая координата движения грузов; С — коэффициент жесткости дерева.
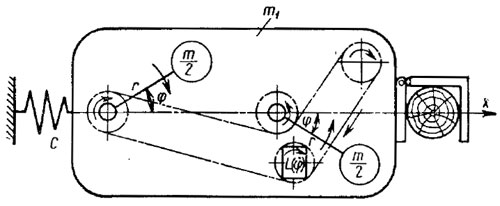
Рис. 46. Схема динамической модели инерционного вибратора
Крутящий момент L(φ) гидромотора через цепные передачи или передачи других видов передается валам с дебалансными грузами. При этом передачи обеспечивают противофазовое синхронное вращение валов и грузов. Из схемы видно, что в системе могут возникать только горизонтальные (название условное в соответствии со схемой) силы инерции по направлению оси х. Так как вибратор (имеется в виду весь узел) закреплен на дереве неподвижно, то возникающие силы инерции от вращения неуравновешенных грузов вызывают горизонтальные колебательные движения дерева вместе с вибратором.
Уравнения Лагранжа II рода, составленные с учетом значений потенциальной и кинетической энергий системы, моментной характеристики L(φ) гидромотора, сил сопротивления вращательному H(φ) и колебательному βχ движениям, имеют вид
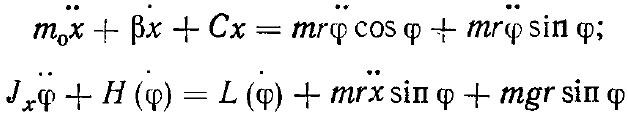
где m0 = m1 + m — обобщенная масса вибратора с деревом и сосредоточенных грузов; Jх —момент инерции вращающихся масс источника энергии.
Проанализировав уравнения с помощью асимптотических методов теории нелинейных колебаний, можно считать, что для инженерных приложений вполне достаточно ограничить анализ первым приближением. Решение уравнений осреднения, которые получают из предыдущих уравнений, дает возможность рассматривать как стационарные, так и переходные процессы.
Введем в полученные уравнения малый параметр ε, который должен удовлетворять условию 0<ε<1. При расчете инерционных вибраторов данного типа малый параметр может быть введен если будут выполнены следующие условия:
![]()
где R — положительное число.
Соблюдение этих условий означает, что силы и моменты в правой части уравнений, а также силы сопротивления (трения) βχ• малы по сравнению с другими силами и моментами, действующими в системе.
Вводя затем новые переменные и производя необходимые преобразования, получаем выражения для определения амплитуды колебательной системы
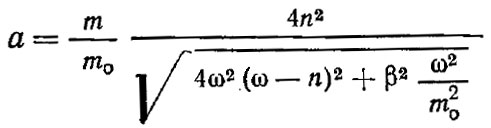
и фазового угла
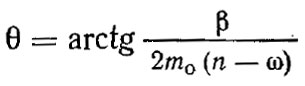
где n — частота вращения гидромотора.
Применяя эти формулы, а также используя известные из теоретической механики соотношения и экспериментальные данные по коэффициентам жесткости деревьев и собственной (свободной) частоте колебательной системы, можно рассчитать инерционный вибратор для колебания штамба плодового дерева.
Максимальную возмущающую силу от вращения неуравновешенных грузов подсчитывают по формуле
Fmax = mvгр2r,
где m — масса двух грузов; vгp = πn/30 — угловая скорость груза; r — расстояние от центра вращения до центра тяжести груза.
Задаваясь массой неуравновешенных грузов, можно получить возмущающую силу, которую они развивают при вращении, или, используя данные по коэффициенту жесткости деревьев, задаются значением возмущающей силы и затем из формулы находят массу неуравновешенных грузов.
На основании теоретических исследований в ВИСХОМе рассчитан оптимальный ряд инерционных вибраторов для колебаний штамбов плодовых деревьев. Техническая характеристика двух вибраторов, изготовленных в ВИСХОМе следующая:
Техническая характеристика инерционных вибраторов
| Малый вибратор ВМ-140 |
Большой вибратор ВБ-250 | |
| Общая масса вибратора,кг | 90 | 250 |
| Масса одного груза, кг | 9,11 | 27,75 |
| Количество пластин в одном грузе |
8 | 10 |
| Габаритные размеры вибратора, мм | ||
| длина |
940 |
1800 |
| ширина | 370 | 700 |
| высота | 220 | 260 |
| Привод неуравновешенных грузов | Гидромотор | МНШ-46 |
| Максимальная частота колебаний, Гц | 27 | 22 |
| Максимальная возмущающая сила, кгс | 1916 | 5440 |
| Собственная частота системы, Гц | 1,5 – 2,0 | 0,9 – 1,2 |
| Максимальная амплитуда колебаний системы в месте обхвата дерева, мм | 30 | 65 |
| Фазовый угол между неуравновешенными грузами, град | 180 | 180 |
Общий вид вибратора ВБ-250 показан на рис. 47.

Рис. 47. Инерционный штамбовый вибратор ВБ-250
Зажимы вибратора ВБ-250 выполнены из двух резиновых труб диаметром 165, толщиной стенки 42,5, длиной 360 мм каждая. Контакт зажимов захвата с деревом осуществляется через двойной резиновый ремень-фартук. Между ремнями фартука может подаваться смазочная жидкость (например, растительное масло) или сухая смазка (например, тальк, отруби и т. п.), что уменьшает до минимума трение ремней между собой. При обжатии штамба вибратор с зажимным устройством из-за конусности дерева или под влиянием других случайных факторов может опускаться вниз, обдирая кору. Наличие же в зажимном устройстве двухслойного резинового фартука, между слоями которого за счет подачи смазки обеспечено минимальное трение, исключает повреждение коры в месте обхвата, так как зажимы (подушки) захвата скользят не по коре дерева, а резина по резине.
С целью использования одного и того же корпуса вибратора для колебания различных штамбов плодовых деревьев неуравновешенные грузы выполнены сложной конфигурации в виде набора пластин. Снятие (добавление) нескольких пластин позволяет получать различную возмущающую силу вибратора Так, каждый груз малого вибратора ВМ-140 состоит из восьми пластин, большого вибратора ВБ-250 — из десяти пластин.
В сезон уборки вибратор ВМ-140 применялся для колебания небольших деревьев с максимальным диаметром штамба 140 мм при захвате на высоте 0,5 м от земли, вибратор ВБ-250 — для колебания деревьев за штамб, диаметр которых достигал 250 мм, при захвате на высоте 0,4 м от земли. Полнота съема на уборке яблок при оптимальном времени колебаний 3 – 5 с получена в пределах 95 – 98%.
Более мощный инерционный штамбовый вибратор (для колебания деревьев диаметром штамба 350 – 400 мм) с двумя массами, вращающимися в противоположных направлениях, изготовлен и установлен на плодоуборочной машине фирмы ПерриХарвестер (США).
Во Франции на самоходной плодоуборочной машине, состоящей из двух секций, каждая из которых оборудована двигателем внутреннего сгорания мощностью 70 л. с., установлен инерционный штамбовый вибратор фирмы Катхал для колебания деревьев с диаметром штамба 350 – 450 мм. Вибратор имеет две вращающиеся в противоположных направлениях массы, расположенные одна над другой. Подобное расположение масс (по французской терминологии) порождает при их вращении «вибрационный ливень» многонаправленных сил инерции.
В Италии разработан инерционный штамбовый вибратор для колебания больших деревьев. Его навешивают на специальное шасси с уширенными шинами, которое оборудовано двигателем внутреннего сгорания мощностью 42 л. с.
Ученые С. Р. Тук и Ф. Р. Браун (США) провели исследование динамики инерционных вибраторов скручивающего действия, т. е. вибраторов, у которых две массы вращаются в одном направлении.
В Среднеазиатском научно-исследовательском институте лесного хозяйства (СредазНИИЛХ) разработан инерционный вибратор для колебания штамбов больших деревьев, особенностью которого являются подпружиненные дебалансные массы. В связи с этим затраты мощности при пуске вибратора в работу незначительные, так как в статическом положении грузы, расположенные на валу, находятся в сбалансированном состоянии относительно центра вращения, и в момент пуска мощность будет потребляться только на преодоление инертности масс и трения в опорах. Под действием инерционной центробежной силы, возникающей при вращении, грузы по направляющим начинают перемещаться в радиальном направлении, если центробежная сила превысит силы сопротивления пружин.
Вибратор, рассчитанный и построенный в СредазНИИЛХ, имеет следующие параметры: масса грузов 50 кг, жесткость пружин 35 кгс/см, максимальный эксцентриситет ротора (вала с грузами) от центра тяжести 72 мм, частота вращения ротора 600, 1250 и 1800 об/мин. При испытаниях вибратора на сборе плодов грецкого ореха были получены хорошие результаты.
В УкрНИИСе разработан инерционный штамбовый стряхиватель, сообщающий дереву круговую вибрацию. Кинематическая схема стряхивателя показана на рис. 48.
Отсылая читателей к работе, в которой подробно изложен аналитический расчет стряхивателя, здесь лишь укажем, что при круговой вибрации амплитуда колебаний штамба дерева
a = mrcv/b,
где m — масса двух дебалансов; rc — суммарный эксцентриситет, равный 2r; v — круговая частота вынужденных колебаний; b — коэффициент сопротивления динамической системы (штамба дерева).
Для создания такой амплитуды колебаний штамбу дерева потребуется мощность, которая определяется из выражения
N = mrcv2a.
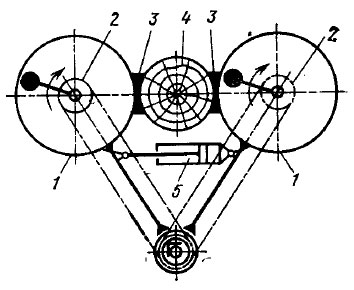
Рис. 48. Кинематическая схема стряхивателя для круговой вибрации штамба дерева:
1 — инерционный вибратор; 2 — цепная передача; 3 — подушки захвата; 4 — штамб дерева; 5 — гидроцилиндр






